A vector is a term which is coined to represent any quantity that has both direction and magnitude. It is taken after the Latin word where a vector means a Carrier. That means a vector needs to carry a quantity from one point to another. For example, if a vector is carrying a point D to a point E, then it is represented as $\vec{DE}$

An important point to be noted is, that these vectors cannot be added algebraically that we use to generally add things in Mathematics. This ought to be added in a geometrical way where even the direction of a vector matters a lot. A vector is generally represented as an arrow with a head and a tail. To add these vectors, we use triangle and parallelogram laws of vectors and we call the result after adding it “Resultant”.

Let us understand and know the different ways adopted for the addition of two vectors.

This is a kind of vector addition where we adopt the triangle law. Triangle Law states that if there are two vectors named $\vec{D}$ and $\vec{E}$ which are marked as DE and EF on the vector plane, where the head of the D vector touches the tail of the E vector, then the addition of these two vectors is the resultant vector $\vec{F}$ represented as DF. 

Here, the vector represented by the line DF is the vector whose tail touches the tail of the $\vec{D}$ vector and whose head touches the head of the $\vec{E}$ vector as shown in the figure.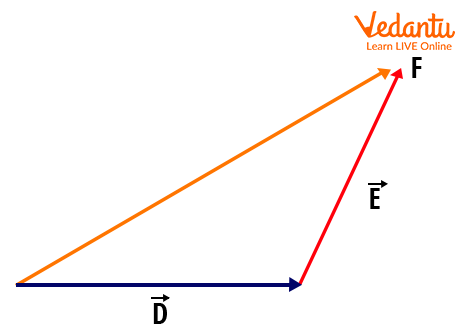

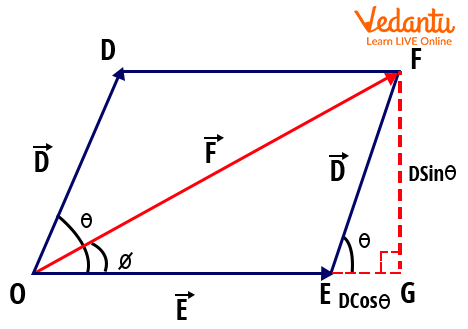
The Triangle Law of Vector Addition 

So here, the magnitude of $\vec{D}+\vec{E}$ is  $\sqrt{d^{2}+e^{2}+2 d e \cos \theta}$

Where d = magnitude of vector $\vec{D}$

             e = magnitude of vector $\vec{E}$ 

             $\theta$ = angle between the two vectors $\vec{D}$ and $\vec{E}$

If the angle between the resultant vector and the vector D is ɸ, then there is this formula stating the relationship between the angle $\theta$ and the magnitude of vectors.

$\tan \phi=\dfrac{e \sin \theta}{d+e \cos \theta}$

This is a kind of vector addition where the parallelogram law is used to add any two vectors. Therefore, Parallelogram law states that “If the two vectors are acting on a point at the same time wherein both of them in magnitude and direction are represented by the two sides of a parallelogram projecting from a point, then their resultant addition vector is represented by the diagonal of the parallelogram both in magnitude and direction.”

Let us demonstrate and understand this law.  

Say, $\vec{D}$ and $\vec{E}$ are the two vectors which are also the two adjacent sides of a parallelogram drawn from a point outward, then the diagonal drawn from the same point is the resultant of these two vectors as shown in the figure.

The Parallelogram Law of Vector Addition

As shown in Figure 2, the triangle OFG makes a right-angled triangle. To find the resultant OF, let’s apply the Pythagoras theorem for the triangle OFG. 

I.e., (OF)2 = (OG)2 + (GF)2    

From the figure, it is obvious that $OG=E+D \cos \theta$ and $GF=D \sin \theta$

Substitute these values in the above equation, and we will get  

$\begin{align} (O F)^{2} &=(E+D \cos \theta)^{2}+(D \sin \theta)^{2} \\ &=E^{2}+D^{2} \cos^{2} \theta+2 D E \cos \theta+D^{2} \sin ^{2} \theta \\ &=E^{2}+D^{2}+2 D E \cos \theta \end{align}$

Therefore, OF can be written as 

$OF=\sqrt{E^{2}+D^{2}+2 E D \cos \theta}$ 

This is the magnitude of the resultant vector that we obtain after adding the vectors $\vec{D}$and $\vec{E}$.  Here $\theta$ is the angle between the two vectors $\vec{D}$ and $\vec{E}$. 

To find the angle between the resultant and the vector $\vec{E}$, which is assumed as ɸ, we use the trigonometric operation tanɸ in the triangle OEG. 

$\tan \phi=\dfrac{F G}{O G}=\dfrac{D \sin \theta}{E+D \cos \theta}$

The above mentioned is the formula of parallelogram law of vector addition. 

Note: The triangle and parallelogram law of vector addition in Mathematics is quite similar to the triangle law of forces and parallelogram law of forces in Physics. The triangle law of forces or the parallelogram law of forces uses the vectors which are represented as physical quantities called Forces.  

Let us look into some solved examples on the triangle or parallelogram law of vector addition.

1. There are two vectors of magnitude 3 units and 4 units between which the angle is 60o. Find the magnitude of the resultant vector using the triangle law of vector addition. 

Solution: The magnitude of the resultant vector is given by the formula $\sqrt{d^{2}+e^{2}+2 d e \cos \theta}$ 

Where |D| = 3 and |E| = 4 and the angle between D and E vectors is 60o 

$|R|=\sqrt{3^{2}+4^{2}+2.3 .4 \cos 60}=1.464$ units.

2. Given that the magnitude of vector D is 5 units and the magnitude of vector E is 7 units. The angle between the two vectors D and E = 30o. Find the angle between the resultant vector and E. 

Solution: Given that |D| = 5 and |E| = 7 and $\theta$ = 30o 

We know the relation from the above diagram in the article, 

$\operatorname{Tan} \phi=\dfrac{F G}{O G}=\dfrac{D \sin \theta}{E+D \cos \theta}$

$\operatorname{Tan} \phi=\dfrac{5 \sin 30}{7+5 \cos 30}$

Therefore, $\phi$ = 17o 

The angle between the resultant and the vector E is 17o

These laws of vector addition are used in various problems where the two vectors are to be added in Mathematics or Physics. Furthermore, the vector addition is commutative and associative as well. Generally, vectors are represented by the addition of three axes components in the XYZ plane. Here, the addition can be done normally as the vectors are represented in the coordinated system. Therefore, the laws of vector addition are demonstrated and proved with thorough apprehension.